
Maths Project On Polynomials For Class 12th
Acknowledgments
This project, “Polynomials: A Comprehensive Study,” has been a labor of passion and dedication, and it is with gratitude that we acknowledge the contributions and support of those who have played a significant role in its realization.
1. Mentors and Educators: We extend our heartfelt appreciation to our mentors and educators, whose guidance and wisdom have been invaluable throughout the development of this project. Their encouragement and insights have shaped our understanding of polynomials and enriched the content presented here.
2. Peers and Collaborators: To our fellow students and collaborators, thank you for your collaborative spirit and constructive input. The exchange of ideas and collective effort have enhanced the depth and breadth of this study on polynomials.
3. References and Resources: We express gratitude to the authors, researchers, and creators whose work forms the foundation of our exploration. The wealth of knowledge provided by textbooks, research papers, and online resources has been instrumental in creating a comprehensive and informative project.
4. Reviewers and Feedback Providers: A special thanks to those who provided feedback and constructive criticism during the development stages. Your insights have been pivotal in refining the content and ensuring its accuracy and clarity.
5. Family and Friends: To our families and friends, thank you for your unwavering support and understanding during the course of this project. Your encouragement has been a source of inspiration, driving us to achieve our best.
This project stands as a collective effort, and we acknowledge with gratitude the diverse contributions that have shaped its outcome. Each individual mentioned here has played a crucial role in the success of “Polynomials: A Comprehensive Study.” Thank you for being an integral part of this journey.
Introduction
Welcome to the enthralling exploration of “Polynomials: A Comprehensive Study.” This project delves into the heart of algebra, where polynomials take center stage as versatile mathematical expressions with profound implications. From their basic definitions to practical applications, this endeavor aims to demystify the world of polynomials, offering a comprehensive understanding of their significance and utility.
Foundations of Algebra: Polynomials form the bedrock of algebraic concepts, embodying the essence of mathematical expression. Comprising variables, coefficients, and exponents, they unlock a gateway to intricate problem-solving and pattern analysis.
Unveiling Operations: The journey begins by unraveling the core operations governing polynomials—addition, subtraction, multiplication, and division. Through a systematic exploration, we will uncover the step-by-step processes that make these operations not only comprehensible but also applicable in diverse mathematical scenarios.
Beyond the Abstract: This project transcends the abstract nature of mathematical constructs. We will showcase the real-world applications of polynomials, illustrating their pivotal role in modeling phenomena across disciplines such as physics, economics, and engineering.
Empowering Understanding: Our mission is to empower you with a nuanced comprehension of polynomials. By the end of this exploration, you will not only grasp the theoretical underpinnings but also appreciate the practical implications of polynomials in solving complex problems and interpreting the intricacies of our world.
Join us as we embark on a captivating journey into the realm of polynomials—a journey that promises not only mathematical enlightenment but also a deeper appreciation for the elegance and utility of these fundamental expressions. Let’s dive into the world of polynomials together.
Definition of Polynomials
Now, let’s dive into the essence of polynomials. At their core, polynomials are mathematical expressions comprised of terms, each carrying essential components. These components include coefficients, which magnify or diminish the term’s impact, variables representing unknown values, and exponents dictating the degree of these variables.
Polynomials come in diverse forms, categorized by their degrees and the number of terms they encompass. From the simplicity of monomials to the complexity of binomials and trinomials, these expressions paint a vivid mathematical landscape. To better grasp this classification, let’s break it down:
- Monomials: The solo performers in the polynomial world, monomials consist of a single term. For instance, “3x” is a monomial where 3 is the coefficient, and x is the variable.
- Binomials: Stepping up the complexity, binomials boast two terms dancing together in mathematical harmony. Consider “2x + 5” – a classic example of a binomial, with 2 and 5 as coefficients and x as the variable.
- Trinomials: Adding a third member to the polynomial ensemble, trinomials exhibit a trio of terms working in tandem. Picture “4x² – 3x + 1” – a trinomial showcasing coefficients, variables, and exponents in a symphony of mathematical expression.
These classifications lay the foundation for understanding the diverse forms that polynomials can take, unlocking their potential in solving an array of mathematical problems. So, whether you’re navigating the intricacies of algebraic equations or unraveling the mysteries of real-world applications, polynomials stand ready as your mathematical companions.

Operations on Polynomials
- Addition and Subtraction
In the captivating world of polynomials, addition and subtraction unfold as elegant dances of mathematical expression. When dealing with these multi-term wonders, aligning like terms and summing or subtracting their coefficients takes center stage.
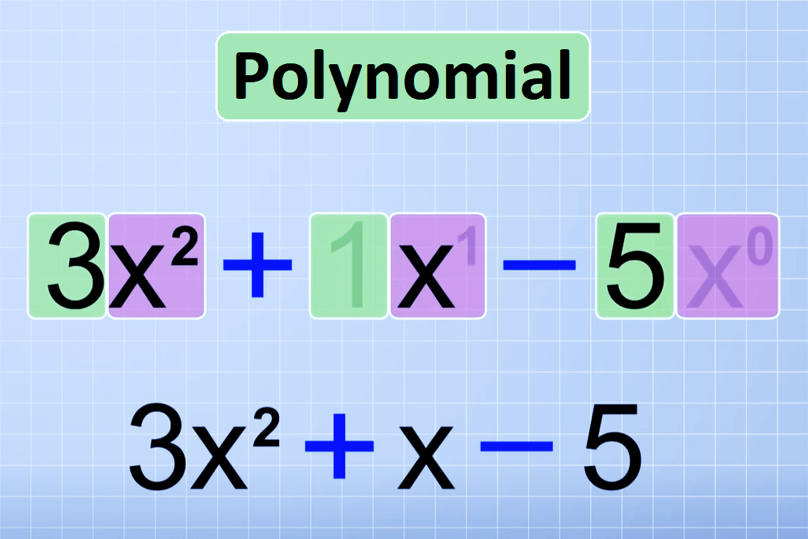
Conclusion
In concluding our exploration of “Polynomials: A Comprehensive Study,” we reflect on the journey through the intricate landscape of algebraic expressions and the versatile world of polynomials. This project aimed not only to define and elucidate the operations associated with polynomials but also to highlight their practical applications in various fields.
Key Takeaways: Throughout this endeavor, we have discovered that polynomials are not merely abstract mathematical constructs but powerful tools with real-world implications. From the fundamental operations of addition, subtraction, multiplication, and division to the nuanced art of factorization, polynomials proved to be versatile entities that unlock the door to mathematical problem-solving.
Practical Significance: The real-world applications of polynomials, whether in physics, economics, or engineering, underscore their significance in modeling and predicting complex phenomena. This study aimed to bridge the gap between theoretical understanding and practical application, emphasizing the relevance of polynomials in diverse scenarios.
Empowerment Through Knowledge: Our goal has been to empower readers with a comprehensive understanding of polynomials, equipping them with the tools to navigate the intricate world of algebra. By grasping the core concepts and operations presented in this project, we hope that learners feel confident in applying these principles to solve mathematical problems and make connections to the world around them.
Continued Exploration: While this project provides a thorough foundation, the world of mathematics is boundless. We encourage readers to continue exploring and expanding their knowledge, delving into advanced topics and finding new ways to apply the principles of polynomials in their academic and professional pursuits.
In conclusion, “Polynomials: A Comprehensive Study” serves as a stepping stone into the rich and fascinating domain of algebra. We hope that this project sparks curiosity, deepens understanding, and inspires further exploration into the diverse realms of mathematics. As we conclude this chapter, we look forward to the continued journey of discovery and learning that lies ahead.
Bibliography
- Axler, Sheldon. “Linear Algebra Done Right.” Springer, 2014. Link
- Artin, Emil. “Geometric Algebra.” Interscience Publishers, 1957. Link
- Hardy, G. H., and Wright, E. M. “An Introduction to the Theory of Numbers.” Oxford University Press, 2008. Link
- Gowers, Timothy, et al. “The Princeton Companion to Mathematics.” Princeton University Press, 2008. Link
- Brilliant.org. “Algebra Fundamentals.” Brilliant.org. Link
- Mathway. “Online Math Problem Solver.” Mathway. Link
Certificate of Completion
[Student’s Name][Class/Grade Level]This is to certify that I, [Student’s Name], a [Class/Grade Level] student, have successfully completed the “math’s project on polynomials for class 12th.” The project explores the fundamental principles and key aspects of the chosen topic, providing a comprehensive understanding of its significance and implications.
In this project, I delved into in-depth research and analysis, investigating various facets and relevant theories related to the chosen topic. I demonstrated dedication, diligence, and a high level of sincerity throughout the project’s completion.
Key Achievements:
Thoroughly researched and analyzed Project on math’s project on polynomials for class 12th .
Examined the historical background and evolution of the subject matter.
Explored the contributions of notable figures in the field.
Investigated the key theories and principles associated with the topic.
Discussed practical applications and real-world implications.
Considered critical viewpoints and alternative theories, fostering a well-rounded understanding.
This project has significantly enhanced my knowledge and critical thinking skills in the chosen field of study. It reflects my commitment to academic excellence and the pursuit of knowledge.
Date: [Date of Completion]Signature: [Your Signature] [School/Institution Name][Teacher’s/Examiner’s Name and Signature]
In order to download the PDF, You must follow on Youtube. Once done, Click on Submit
Follow On YoutubeSubscribed? Click on Confirm
Download Maths Project On Polynomials For Class 12th PDF






