
Physics Project On ‘Gauss Theorem’ For Class 12
Acknowledgment
I’d like to take a moment to extend my heartfelt gratitude to some incredible folks and resources that played a pivotal role in bringing this Gauss’s Theorem project to a triumphant close.
First and foremost, a massive shout-out to my physics mentor, [Teacher’s Name]. Their guidance, endless patience, and sheer brilliance were like a guiding light through the twists and turns of this project. They not only helped me make sense of this intricate subject but also welcomed my countless questions with open arms.
I can’t forget my fantastic classmates. Our enlightening discussions and brainstorming sessions were like refining fire for the ideas and content presented in this project. Teamwork truly makes the dream work.
My family deserves a special mention. Their unwavering support and understanding throughout this project have been my rock. Their faith in my abilities has been a constant source of inspiration and motivation.
Huge props to the authors of those textbooks and research papers I delved into for reference and insight. Their groundbreaking work laid the groundwork for my research and provided those essential ‘Aha!’ moments.
Last but not least, kudos to the online academic community. You folks offered a treasure trove of resources and engaging discussions about all things Gauss’s Theorem. You’re the unsung heroes in this academic journey.
To each and every one of you, I extend my heartfelt thanks. Your support and encouragement have been the driving force behind the triumphant completion of this project.
With gratitude,
[Your Name]Introduction to Gauss’s Theorem
Let’s dive into the fascinating realm of Gauss’s Theorem, a mathematical gem that goes by another moniker, Gauss’s Divergence Theorem. This concept isn’t just any run-of-the-mill idea; it’s a cornerstone of vector calculus and electromagnetism, holding the key to unlocking the secrets of electric and magnetic fields in our three-dimensional universe. And, of course, we tip our hats to none other than the brilliant Carl Friedrich Gauss for giving it his name.
So, what’s the scoop on Gauss’s Theorem? Well, imagine it as a bridge—a powerful, mathematical bridge—that connects the behavior of a vector field (like those electric and magnetic fields we’re always talking about) inside a closed space to what’s happening on the surface that wraps around that space. It’s like peeking inside a magic box and understanding how the magic works on the outside.
Now, why is this theorem such a rock star in the world of physics, especially when we’re talking about electromagnetism? The answer is versatility. Gauss’s Theorem steps up to the plate in a wide array of scenarios, helping us untangle the mysteries of complex electromagnetism problems.
At its core, this theorem waltzes through the notion of flux. Flux, in this context, is all about measuring how a vector field flows through a surface. When we apply this concept to electric fields, it lets us in on the secret of how electric charges organize themselves within a closed space and how that arrangement influences the electric field at various points inside. And guess what? It does a similar magic trick with magnetic fields, revealing how magnetic sources pull the strings of those field lines within a closed region.
So there you have it, Gauss’s Theorem in a nutshell—a mathematical tour de force that helps us decode the intricate dance of electric and magnetic fields in the vast canvas of three-dimensional space.
Gauss’s Law
Gauss’s Law, a true heavyweight in the world of electromagnetism, is like the close cousin of Gauss’s Theorem. This powerhouse principle is your go-to tool for unraveling the mysteries of electric fields caused by electric charges. All thanks to the mathematical genius Carl Friedrich Gauss for giving us this gem.
Now, let’s get down to the nitty-gritty with Gauss’s Law. This law is all about giving us the mathematical scoop on how electric charges are distributed and how they create those electric fields that surround them.
The Mathematical Magic of Gauss’s Law:
Gauss’s Law, in its mathematical glory, looks like this:
∮E⋅dA = (Q_enclosed) / ε₀
Here’s the lowdown on the lingo:
- ∮E⋅dA is a fancy way of saying we’re doing a surface integral of the electric field E over a closed surface.
- Q_enclosed is the total electric charge hanging out inside that closed surface.
- ε₀ (epsilon naught) is the electric constant, also known as vacuum permittivity, clocking in at roughly 8.854 x 10⁻¹² C²/N·m² in SI units.
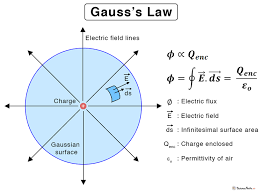
Cracking the Code of Gauss’s Law:
What Gauss’s Law is spilling the beans on is this: The total electric flux (which is basically the integral of the electric field over a closed surface) equals the sum total of electric charge sealed up within that surface, all divided by ε₀. It’s like counting the number of electric field lines that either start from or end on electric charges.
Now, let’s wrap our heads around a few key points:
- Flux and Electric Field: Electric flux measures how many electric field lines cozy up to a closed surface. The law tells us how this is connected to the charge inside and gives us a glimpse into the electric field’s strength and direction.
- Closed Surfaces: Gauss’s Law loves to work with closed surfaces. These surfaces are chosen carefully to make our math easy-peasy, based on how the charges are spread out.
- Symmetry: When dealing with charge distributions that are all neat and symmetric, like spheres, cylinders, or planes, Gauss’s Law is your superhero. It turns complex electric field calculations into a walk in the park.
Where Gauss’s Law Shines:
- Electric Field of Point Charges: Gauss’s Law is your buddy when figuring out the electric field due to point charges, whether it’s one charge or a bunch of them.
- Electric Field of Symmetric Charge Distributions: It’s like a secret shortcut for calculating electric fields when things are all symmetric, like charged spheres or infinite planes.
- Detecting Charge Distributions: When you know the electric field, Gauss’s Law can help you play detective and find out how the charges are distributed inside a closed surface.
- Charge Conservation Checks: It’s the lie detector test for electric charge conservation within a closed area.
Closed Surfaces and the Dance of Electric Charges
In the magnificent world of Gauss’s Law and its electrifying applications, grasping the concept of closed surfaces and the art of arranging electric charges is absolutely key. These two pieces of the puzzle are like the dynamic duo in our quest to unlock the secrets of electric fields. So, let’s dive into the details:
Closed Surfaces:
Picture a closed surface as a magical three-dimensional boundary that wraps itself around a specific chunk of space. It’s like a cosmic fence that separates the zone we’re interested in from the great beyond. When we’re wielding Gauss’s Law, we’re pretty picky about which closed surface to choose. It’s all about making our math as smooth as silk, and we often pick surfaces that match the charge distribution’s symmetry. Think spheres, cylinders, and cubes for starters.
Charge Distributions:
Charge distributions are like the choreography of electric charges within a designated area of space. They can take on various forms, like point charges (those solo acts), line charges (the linear performers), surface charges (the ones spread out like a canvas), or volume charges (the stars of the show). Why do they matter? Well, they’re the architects of the electric field in town.
Now, let’s connect the dots between these concepts and Gauss’s Law:
Picking the Right Closed Surface: When we’re throwing Gauss’s Law into action, the first order of business is choosing the perfect closed surface. We’re matchmakers here, pairing the surface with the symmetry of the charge distribution. For instance:
- For a single point charge, we often go for a spherical closed surface centered on the charge because it’s beautifully spherical.
- When we’re dealing with an infinite plane packed with charges, a cylindrical closed surface with one end kissing the plane is our go-to choice. Why? Symmetry, my friend.
Cracking the Code of Electric Flux: Gauss’s Law connects the total electric flux (that’s the integral of the electric field over the closed surface) to the net charge cozying up inside the surface. It’s like counting the electric field lines that pass through the surface and relating them to the charge inside the cosmic boundary.
Symmetry the Simplifier: Choosing a closed surface that’s symmetrical to the charge distribution is like finding a shortcut in a maze. In these cases, the electric field often behaves like a well-behaved child, being consistent in magnitude and direction across the closed surface. This makes calculating flux a breeze.
A Law for All Seasons: Gauss’s Law isn’t picky. It plays nice with all kinds of charge distributions. Whether it’s a point charge, a charged sphere, an endless charged wire, or any other electric charge scenario, Gauss’s Law can step in and reveal the electric field’s secrets.
Detective Work: In some situations, Gauss’s Law can even be flipped around. If we know the electric field, it can lend a hand in figuring out the charge distribution within a closed surface. It’s like solving a mystery in reverse.
Gauss’s Theorem
Gauss’s Theorem, also affectionately known as Gauss’s Divergence Theorem, is like a magical wand in the world of electromagnetism. It’s the brainchild of none other than the genius Carl Friedrich Gauss, and it’s the key that unlocks the mysteries of electric fields by dancing with electric charges within a closed volume. Let’s dive into the enchanting realm of Gauss’s Theorem for electric fields:
The Mathematical Charm of Gauss’s Theorem for Electric Fields:
Gauss’s Theorem elegantly states:
∮E⋅dA = (1 / ε₀) ∫∫∫ρ dV
Let’s break it down:
- ∮E⋅dA is like a fancy way of saying we’re doing a surface integral of the electric field E over a closed surface.
- ε₀ (epsilon naught) is our mystical constant, also known as vacuum permittivity, which stands at approximately 8.854 x 10⁻¹² C²/N·m² in SI units.
- ∫∫∫ρ dV is our volume integral of charge density ρ, covering the closed volume embraced by that surface.
Decoding Gauss’s Theorem for Electric Fields
What this theorem is whispering to us is this: The total electric flux (that’s the integral of the electric field over the closed surface) is like a cosmic bill, and it equals the total electric charge tucked away inside that cosmic surface, all divided by ε₀. It’s like tallying how many electric field lines start or end on electric charges within a sealed region.
Now, let’s shine a light on some key insights:
- Flux and Electric Field: The left side of our equation (∮E⋅dA) is all about electric flux—it measures how electric field lines cross a closed surface, like counting sunbeams through a window.
- Charge Density: On the right side (∫∫∫ρ dV), we’re digging into the charge density ρ. It tells us how electric charges are scattered within the closed volume, like a treasure hunt for electric charge.
- The Magic ε₀: ε₀, our trusty constant, makes sure the units of charge and electric field play nicely together. It’s the glue that holds the equation’s dimensions in place.
Where Gauss’s Theorem Shines for Electric Fields
- Electric Fields of Symmetry: Gauss’s Theorem really struts its stuff when we’re dealing with symmetrical charge setups, think charged spheres or fancy cylinders. In these cases, it’s like the math fairy granting our wishes for simplified electric field calculations.
- Gauss’s Law Validation: Gauss’s Theorem is the rock-solid foundation upon which Gauss’s Law stands. When we use it on a surface that’s shielding no charge (∫∫∫ρ dV = 0), Gauss’s Theorem nods in agreement with Gauss’s Law, which tells us the electric field divergence is zilch where no charges roam.
- Peeking Inside Enclosures: The theorem gives us a backstage pass to understand how electric field lines swirl and twirl around various charge collections enclosed by surfaces, and how those tucked-away charges call the shots.
Examples and Problem Solving
Let’s Solve Some Electric Field Mysteries: Examples and Problem-Solving
To truly wrap our heads around Gauss’s Theorem for electric fields, we’re diving into the exciting world of real-world examples and solving problems that put this theorem to work. Get ready for some illuminating scenarios:
Example 1: The Electric Field of a Point Charge
Scenario: Imagine we’ve got a point charge ‘Q’ hanging out at a distance ‘r’ from us, and we want to figure out the electric field it’s creating using Gauss’s Theorem.
Solution:
- We start by picking a closed surface that wraps around our point charge. In this case, a spherical surface centered on the charge is perfect because it’s symmetrical.
- We roll out Gauss’s Theorem and calculate the electric flux (∮E⋅dA) across our spherical surface.
- Since the electric field behaves the same in all directions (radially symmetric), the math simplifies. We look at E⋅dA as E * dA * cos(θ), where θ is the angle between the electric field and the surface’s normal.
- Now, we find the electric field’s magnitude on our spherical surface: E = (Q_enclosed) / (4πε₀r²).
- Let’s integrate and calculate the flux over the spherical surface.
- Finally, we set the flux equal to the right side of Gauss’s Theorem and solve for our electric field ‘E.’
Example 2: The Electric Field of an Infinite Charged Plane
Scenario: We’re standing a distance ‘d’ away from an infinite charged plane with a uniform charge density ‘σ,’ and we’re curious about the electric field at point ‘P.’ Gauss’s Theorem to the rescue!
Solution:
- To make our lives easier, we choose a Gaussian surface that plays nicely with the problem’s symmetry. In this case, a cylindrical Gaussian surface perpendicular to the plane and centered at ‘P’ fits the bill.
- We put Gauss’s Theorem to work again, this time calculating the electric flux (∮E⋅dA) through our cylindrical surface.
- We peek inside our Gaussian surface to find the enclosed charge, which is Q_enclosed = σ * A, with ‘A’ as the circular end’s area of the cylinder.
- The electric field here points straight through our cylindrical surface, so E⋅dA is just E * dA.
- We express the flux in terms of the electric field and the cylinder’s surface area.
- Next, we equate the flux to the right side of Gauss’s Theorem and work our magic to find the electric field ‘E’ at point ‘P.’
Problem-Solving Wisdom:
- Symmetry is your best friend; choose Gaussian surfaces that make the math simpler.
- Never forget to spot the charge lurking inside your chosen Gaussian surface.
- Keep units and constants like ε₀ in check for a hassle-free solution.
- A keen eye for detail in your mathematical steps ensures accuracy.
- Visualize the problem using diagrams; it makes everything clearer.
Applications in Electromagnetism
The Versatility of Gauss’s Theorem in Electromagnetism
Gauss’s Theorem isn’t just a mathematical gem; it’s the secret weapon in the world of electromagnetism. This versatile tool simplifies the complex and untangles the mysteries of electric and magnetic fields. Let’s uncover its applications in the realm of electromagnetism:
Electric Flux and Gauss’s Law:
- Gauss’s Law for Electricity: Gauss’s Theorem is the star player in Gauss’s Law for electricity. It’s the key to finding electric fields from various charge distributions, from simple point charges to the intricate geometry of charged spheres and infinite planes. This law is the backbone of understanding how electric fields influence charges and the workings of electric circuits.
Electric Field of Symmetric Charge Distributions:
- Charged Spheres: Gauss’s Theorem makes light work of calculating the electric field both inside and outside charged conducting spheres. This is essential for understanding the behavior of conductors and their interactions with electric fields.
Electric Field of Infinite Planes:
- Uniformly Charged Infinite Planes: Ever wondered about the electric field near and far from an infinite uniformly charged plane? Gauss’s Theorem is the compass guiding us through this exploration. It’s vital for understanding how electric fields behave near vast conducting surfaces, like Earth’s surface during lightning strikes.
Electric Field in Insulating Materials:
- Dielectrics: Gauss’s Theorem is our guide when electric fields penetrate insulating materials (dielectrics). It helps us understand how electric fields are affected by induced charges on the dielectric’s surfaces. This knowledge is crucial in the study of capacitors and the behavior of dielectric materials.
Electric Field and Symmetry:
- Symmetric Charge Distributions: Gauss’s Theorem is at its best when tackling symmetric charge arrangements. Whether it’s spheres, cylinders, or planes, it simplifies electric field calculations and is a go-to tool for solving real-world problems.
Magnetic Field of Permanent Magnets:
- Gauss’s Law for Magnetism: Although magnetic monopoles don’t exist, Gauss’s Theorem still has a role to play in certain magnetic field scenarios. Gauss’s Law for Magnetism tells us that magnetic field lines always form closed loops. It’s this theorem that helps us understand why there are no isolated magnetic charges and why the total magnetic flux through a closed surface is always zero.
Magnetic Field of Symmetric Current Distributions:
- Ampère’s Law: Gauss’s Theorem teams up with Ampère’s Law to uncover the magnetic field around symmetric current distributions. Think long straight wires or solenoids. This duo is essential for designing electromagnets and deciphering magnetic field behaviors in circuits.
Applications in Electromagnetic Theory:
- Maxwell’s Equations: Gauss’s Theorem isn’t just a side character; it’s a foundational element of Maxwell’s equations. These four equations are the heartbeat of electromagnetic theory. Gauss’s Theorem provides the mathematical groundwork for these equations, allowing us to harmoniously describe all things electromagnetic.
Limitations and Assumptions
As we harness the power of Gauss’s Theorem in the electrifying world of electromagnetism, it’s crucial to be aware of its limitations and the assumptions it carries. Let’s shine a light on these caveats to ensure the theorem’s accuracy and relevance in practical applications. Here are the key points to bear in mind:
- Closed Surfaces: Gauss’s Theorem is your trusty sidekick for closed surfaces. It doesn’t play well with open surfaces or those that stretch out into the infinite unknown. So, always choose a closed surface for Gauss’s Theorem to work its magic.
- Symmetry: Gauss’s Theorem thrives on symmetry. It’s at its peak when dealing with symmetric charge or current distributions. When symmetry takes a back seat, applying the theorem can be a bit of a puzzle, requiring a breakdown into more symmetric components.
- Charge Distribution: Gauss’s Theorem assumes a continuous charge distribution. It loves the macroscopic, continuous world but might stumble when dealing with discrete charges or ultra-fine-grained distributions like individual electrons.
- Charge Conservation: Implicitly, the theorem assumes the conservation of electric charge. It doesn’t handle scenarios involving changing charge distributions or non-conservative systems where charges might pop in or vanish.
- Linearity of Electric Fields: Gauss’s Theorem believes in the power of superposition. It assumes that the total electric field at a point is the sum of the electric fields from individual charges or charge distributions. But in exotic realms near black holes or within quantum electrodynamics, this assumption might not hold.
- Electrostatic Conditions: Gauss’s Theorem is in its element in electrostatic scenarios, where charges are peacefully at rest. In dynamic situations with changing electric and magnetic fields, this theorem might not be the hero you need. Maxwell’s equations, the extended version, would be your go-to.
- Absence of Magnetic Monopoles: Gauss’s Theorem takes a firm stance against magnetic monopoles. It believes in the cosmic balance, where magnetic field lines always form loops, and there are no lone magnetic charges. This is a fundamental pillar of electromagnetic theory.
- Continuity and Differentiability: Gauss’s Theorem speaks the language of continuity and differentiability. It assumes that electric fields and charge densities within the chosen volume are well-behaved. If there are abrupt changes or singularities, the theorem might raise an eyebrow.
Gauss’s Theorem and Maxwell’s Equations
In the grand symphony of classical electromagnetism, Gauss’s Theorem takes center stage, serving as the pivotal link that connects us to Maxwell’s equations. These equations are the bedrock of our understanding of how electric and magnetic fields dance in response to charges and currents. Let’s explore the profound connection between Gauss’s Theorem and two of Maxwell’s equations: Gauss’s Law for Electricity and Gauss’s Law for Magnetism.
Gauss’s Law for Electricity:
- Gauss’s Theorem Connection: Gauss’s Theorem lays the very groundwork for Gauss’s Law for Electricity, also known as Gauss’s first equation. This law elegantly tells us that the electric flux through a closed surface is intimately tied to the total electric charge enclosed within that surface. Mathematically, it whispers:
∮E⋅dA = (1 / ε₀) ∫∫∫ρ dV - Maxwell’s Equation: Within the sacred text of Maxwell’s equations, Gauss’s Law for Electricity is one of the cornerstones. It quantifies how electric fields emerge from electric charges and how the electric field’s divergence is influenced by the charge density (ρ).
Gauss’s Law for Magnetism:
- Gauss’s Theorem Connection: While not a direct offspring of Gauss’s Theorem, Gauss’s Law for Magnetism pays homage to it. It states that magnetic field lines are eternal loops, with no solo magnetic charges wandering the universe. Thus, the total magnetic flux through any closed surface forever remains at zero.
- Maxwell’s Equation: This law finds its home in Maxwell’s equations as well. Formally, it is presented as:
∮B⋅dA = 0 - Ampère’s Circuital Law: To complete the tale of magnetic forces, we turn to Ampère’s Circuital Law, another luminary in Maxwell’s equations. It narrates how magnetic fields circulate and interact with electric currents.
Connection to the Entire Maxwell’s Equations:
- Holistic Understanding: While Gauss’s Theorem graciously lends its wisdom to Gauss’s Laws, the full ensemble of Maxwell’s equations comprises four harmonious equations. Alongside Gauss’s Laws, we have Faraday’s Law of Electromagnetic Induction and the Ampère-Maxwell Law.
- Comprehensive Description: These four equations weave a tapestry that captures the essence of electromagnetic phenomena. They reveal how electric and magnetic fields are born, how they traverse space, and how they react to the ebb and flow of charges and currents.
Conclusion
In our journey through the intricate realms of electromagnetism, we’ve ventured deep into the heart of Gauss’s Theorem and its profound applications. This exploration has illuminated the core principles, mathematical intricacies, and practical significance of this fundamental theorem, paying homage to its namesake, Carl Friedrich Gauss. As we conclude, let’s recap the pivotal insights gleaned from our odyssey:
Foundations of Gauss’s Theorem:
- Gauss’s Theorem, or Gauss’s Divergence Theorem, is the compass guiding our understanding of electric and magnetic fields. It unveils the intrinsic relationship between the flux of a vector field (such as electric or magnetic fields) across a closed surface and the field’s divergence within an enclosed volume.
Mathematical Formulation:
- In the realm of electric fields, Gauss’s Theorem is elegantly inscribed as ∮E⋅dA = (1 / ε₀) ∫∫∫ρ dV, where E denotes the electric field, ε₀ stands as the electric constant, ρ signifies the charge density, and the integrals sweep across a closed surface and its enshrined volume.
Electric Field Chronicles:
- Gauss’s Theorem’s prowess shines when discerning electric fields arising from diverse charge distributions. It unveils the secrets behind point charges, charged spheres, and infinite planes, offering clarity in the realm of electrostatics.
- Symmetry becomes our ally, simplifying calculations and rendering Gauss’s Theorem indispensable in scenarios adorned with geometric harmony.
Magnetic Fields and the Gauss’s Embrace:
- While magnetic fields also engage with Gauss’s Theorem, they do so with the caveat of a magnetic monopole-free universe. It proclaims that the sumptuous magnetic flux through any closed surface forever dances to the tune of zero.
Harmonious Overture to Maxwell’s Equations:
- Gauss’s Theorem extends its benevolence to the illustrious Maxwell’s equations, particularly enfolding Gauss’s Laws for Electricity and Magnetism within its mathematical embrace.
- These equations, born of the union between Gauss’s wisdom and the principles of electromagnetism, unveil the intimate connection between electric and magnetic fields, charges, and currents.
Limits and Assumptions:
- Every theorem, no matter how profound, bears limitations. Gauss’s Theorem finds its boundaries, often in the form of closed surfaces and the refuge of symmetry.
Electromagnetic Terrain Exploration:
- In the grand tapestry of electromagnetism, Gauss’s Theorem finds its purpose in an array of applications. It unravels the mysteries of electric and magnetic fields around charges, conductors, dielectrics, and the enchanting realm of current-carrying wires.
Certificate of Completion
[Student’s Name][Class/Grade Level]This is to certify that I, [Student’s Name], a [Class/Grade Level] student, have successfully completed the project on ” Gauss Theorem For Class 12.” The project explores the fundamental principles and key aspects of the chosen topic, providing a comprehensive understanding of its significance and implications.
In this project, I delved into in-depth research and analysis, investigating various facets and relevant theories related to the chosen topic. I demonstrated dedication, diligence, and a high level of sincerity throughout the project’s completion.
Key Achievements:
Thoroughly researched and analyzed Physics Project On ‘Gauss Theorem’ For Class 12.
Examined the historical background and evolution of the subject matter.
Explored the contributions of notable figures in the field.
Investigated the key theories and principles associated with the topic.
Discussed practical applications and real-world implications.
Considered critical viewpoints and alternative theories, fostering a well-rounded understanding.
This project has significantly enhanced my knowledge and critical thinking skills in the chosen field of study. It reflects my commitment to academic excellence and the pursuit of knowledge.
Date: [Date of Completion]Signature: [Your Signature] [School/Institution Name][Teacher’s/Examiner’s Name and Signature]
In order to download the PDF, You must follow on Youtube. Once done, Click on Submit
Follow On YoutubeSubscribed? Click on Confirm
Download Physics Project On ‘Gauss Theorem’ For Class 12 PDF






